Calculation of electrical loads

Determination of maximum loads by the demand factor method

This method is the simplest and boils down to calculating the maximum active load using the formula:

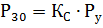
The demand coefficient method can be used to calculate loads for those separate groups of electricity consumers, workshops and enterprises in general, for which there is data on the value of this coefficient (see Coefficients for calculating electrical loads).

When calculating the loads for individual groups of electric receivers, this method is recommended to be used for those groups whose electric receivers work with a constant load and with a duty factor equal to (or close to) one, such as electric motors of pumps, fans and others.

According to the P30 value obtained for each group of electrical consumers, the reactive load is determined:

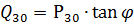
moreover, tanφ is determined by the cosφ characteristic of a given group of electrical consumers.

The active and reactive loads are then summed separately and the total load is found:

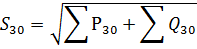
The loads ΣP30 and ΣQ30 are the sums of the maximum values ​​for individual groups of electrical consumers, while in fact the maximum amount must be determined. Therefore, when determining the loads of a network section with a large number of different groups of electrical receivers, the coefficient of combining the maxima KΣ must be introduced, i.e.

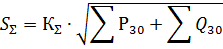
The value of KΣ is in the range of 0.8 to 1, and the lower limit is usually taken when calculating the loads in the whole plant as a whole.

For separate electrical receivers high power, as well as for energy users, rarely or even for the first time in the design practice, the demand factors should be identified by clarifying the actual load factors together with the technologists.

Determination of maximum loads by the method of double expression

This method was proposed by Ing. DS Livshits initially for determining the design loads for electric motors of the individual drive of metalworking machines, and then it was extended to other groups of electric receivers.

According to this method, the half-hourly maximum active load for a group of electrical consumers with the same operating mode is determined by the expression:

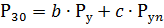
where Рn — installed capacity of the largest energy consumers, b, c — coefficients that are constant for a certain group of energy consumers under the same operating mode.

According to the physical sense, the first member of the calculation formula determines the average power, and the second - the additional power that can occur within half an hour as a result of the coincidence of the maximum load of the individual electrical consumers of the group. Therefore:

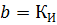
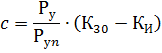
It follows that for small values ​​of Pp compared to Ru, which happens with a large number of electric receivers of more or less the same power, K30 ≈ CP, and the second term of the calculation formula can be neglected in such cases, assuming P30 ≈ bPp ≈ Psr.cm. On the contrary, with a small number of electric receivers, especially if they differ sharply in power, the influence of the second term in the formula becomes very significant.

Calculations using this method are more cumbersome than using the demand factor method. Therefore, the use of the double expression method is justified only for groups of energy consumers operating with a variable load and with low switching coefficients, for which the demand coefficients are either absent at all or can lead to erroneous results. In particular, for example, it is possible to recommend the use of this method for electric motors of metalworking machines and for electric resistance furnaces of small power with periodic loading of products.

The method for determining full load S30 using this method is similar to that described for the demand factor method.

Determination of maximum loads by the method of the effective number of energy consumers.

The effective number of electrical receivers is understood as the number of receivers, equal in power and homogeneous in operating mode, which determines the same value of the calculated maximum as a group of receivers with different power and operating mode.

The effective number of energy consumers is determined by the expression:

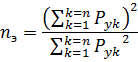
The largest sun and the utilization factor corresponding to this group of electric receivers, according to the reference tables, the maximum factor of KM and then the half-hour maximum of the active load are determined

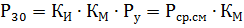
In order to calculate the load of each group of electric receivers with the same operating mode, the determination of PE makes sense only if the electric receivers included in the group differ significantly in power.

With the same power p electrical receivers included in the group

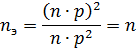
i.e. the effective number of electric motors is equal to the actual number. Therefore, with the same or slightly different capacities of the power consumers of the group, it is recommended to determine the CM according to the actual number of power consumers.

When calculating the load for several groups of electrical receivers, it is necessary to determine the average value of the utilization factor using the formula:

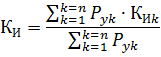
The method of the effective number of electric receivers is applicable to any group of electric receivers, including intermittently operated electric receivers. In the latter case, the installed power Ru is reduced to duty cycle = 100%, i.e. to continuous operation.

The effective number of users method is better than the other methods because the maximum factor, which is a function of the number of users, is involved in determining the load.In other words, this method calculates the maximum of the sum of the loadings of individual groups, and not the sum of the maxima, as is the case, for example, with the search coefficient method.

To calculate the reactive component of the load Q30 from the found value of P30, it is necessary to determine tanφ. For this purpose, it is necessary to calculate the average load for each group of electrical consumers and determine tanφ from the ratio:

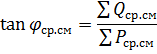
Returning to the definition of PE, it should be noted that with a large number of groups and different capacities of individual electric receivers in the groups, finding ΣPy2 turns out to be practically unacceptable. Therefore, a simplified method is used to determine pe depending on the relative value of the affective number of electrical receivers pe = ne / n.

This number is found from reference tables, depending on the ratios:

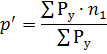
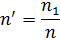
where n1 is the number of electrical receivers, each of which has a capacity of at least half of the power of the most powerful electrical receiver, ΣPupg1 is the sum of the installed powers of these electrical receivers, n — the number of all electrical consumers, ΣPу — the sum of the installed powers of all electrical consumers.

Determination of maximum loads based on specific norms of electricity consumption per unit of production

To have information about the planned productivity of the enterprise, workshop or technological group of receivers and for specific consumption of active energy per unit of production, you can calculate the maximum half-hourly active load using the expression,

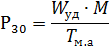
where Wyd is the specific energy consumption per ton of product, ME the annual production, Tm.a — the annual number of hours of use of the maximum active load.

In this case, the full load is determined based on the weighted average annual power factor:

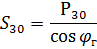
This method of calculation can be used to roughly determine the loads for enterprises as a whole or for individual workshops that produce finished products. To calculate the loads on individual sections of electrical networks, the use of this method, as a rule, turns out to be impossible.

Specific cases of determining the maximum loads with the number of energy consumers up to five

Counting the loads of groups with a small number of energy consumers can be done in the following simplified ways.

1. If there are two or three electrical receivers in the group, the sum of the rated power of the electrical receivers can be taken as the calculated maximum load:

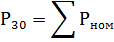
and therefore

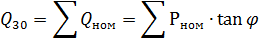
For electric receivers, which are homogeneous in type, power and mode of operation, the arithmetical addition of the total powers is permissible. Then,

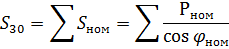
2. If there are four or five electric receivers of the same type, power and operating mode in the group, the maximum load can be calculated based on the average load factor, and in this case the arithmetic sum of the total powers can be assumed to be:

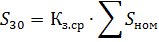
3. With the same number of different types of electrical receivers, the calculated maximum load must be taken as the sum of the products of the rated power of the electrical receivers and the load factors characteristic of these electrical receivers:

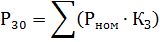
and therefore:

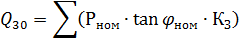
Determination of maximum loads in the presence of a group, together with three-phase, also single-phase consumers of electricity

If the total installed power of stationary and mobile single-phase electric receivers does not exceed 15% of the total power of three-phase electric receivers, then the entire load can be considered three-phase, regardless of the degree of uniformity of the distribution of single-phase loads in phases.

Otherwise, that is, if the total installed power of single-phase power consumers exceeds 15% of the total power of three-phase power receivers, the distribution of single-phase loads by phases must be carried out in such a way that the greatest degree of uniformity is achieved.

When this succeeds, the load counting can be done in the usual way, but if not, then the counting must be done for the most loaded phase. In this case, two cases are possible:

1. all single-phase electric consumers are connected to phase voltage,

2. among the single-phase electric receivers there are also those that are connected to mains voltage.

In the first case, for the installed power, one third of their actual power must be taken for groups of three-phase electric receivers (if any), for groups of single-phase electric receivers - the power connected to the most loaded phase.

According to the phase powers obtained in this way, the maximum load of the most loaded phase is calculated in each of the ways and then, multiplying this by 3, the load of the three-phase line is determined.

In the second case, the most loaded phase can be determined only by calculating the average powers for which the single-phase loads connected to the network voltage must be brought to the corresponding phases.

Reduced to phase a, the active power of single-phase receivers connected, for example, between phases ab and ac, is determined by the expression:

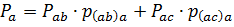
Accordingly, the reactive power of such receivers

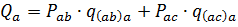
here Рab, Ras are the powers connected to the line voltage, respectively between the phases ab and ac, p (ab) a, p (ac) a, q (ab) a, q (ac) a, are the coefficients of bringing the loads, connected to the line voltage, to phase A.

By circularly rearranging the indices, expressions can be obtained to give the power to each phase.