Why complex numbers are used for calculations in AC circuits

As you know, complex numbers are used to solve some typical problems in electrical engineering. But what are they used for and why is it done this way? This is what we will try to understand in the course of this article. The fact is that the complex method or the method of complex amplitudes is convenient for calculating complex AC circuits. And to begin with, let's recall some basics of mathematics:

As you can see, the complex number z includes the imaginary part and the real part, which differ from each other and are denoted differently in the text. The complex number z itself can be written in algebraic, trigonometric or exponential form:

Historical background

It is believed that the idea of ​​imaginary numbers began in 1545, when the Italian mathematician, engineer, philosopher, physician and astrologer Girolamo Cardano published this method of solving equations in his treatise "The Great Art", where, according to among others , he admitted that Niccolò had given him the idea to Tartaglia (an Italian mathematician) 6 years before the publication of this work. In his work, Kradano solves equations of the form:

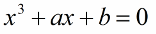
In the process of solving these equations, the scientist was forced to admit the existence of some «unreal» number, the square of which will be equal to minus one «-1», that is, as if there is a square root of a negative number, and if it is now squared, will turn out to be the corresponding negative number under the root. Cardano stated the rule of multiplication, according to which:

For three centuries, the mathematical community was in the process of getting used to the new approach proposed by Cardano. Imaginary numbers are gradually taking root, but mathematicians are reluctant to accept. It wasn't until the publication of Gauss's works on algebra, where he proved the fundamental theorem of algebra, that complex numbers were finally fully accepted, the 19th century was at hand.

Imaginary numbers became a real lifesaver for mathematicians because the most complex problems became much easier to solve by accepting the existence of imaginary numbers.

So it soon came to electrical engineering. AC circuits were sometimes very complex and many integrals had to be calculated to calculate them, which was often very inconvenient.

Finally, in 1893, the brilliant electrical engineer Carl August Steinmetz spoke in Chicago at the International Electrotechnical Congress with a report "Complex numbers and their application in electrical engineering", which actually marked the beginning of the practical application by engineers of the complex method of calculating electric circuits for AC current.

We know this from the physics course alternating current — this is a current that changes over time in both magnitude and direction.

In technology, there are different forms of alternating current, but the most common today is alternating sinusoidal current, this is what is used everywhere, with the help of which electricity is transmitted, in the form of alternating current, which is generated, converted by transformers and is consumed by loads. A sinusoidal current changes periodically according to a sinusoidal (harmonic) law.

The effective values ​​of the current and voltage are less than the amplitude values ​​of the root of two times:

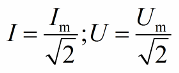
In the complex method, the effective values ​​of currents and voltages are written as follows:

Note that in electrical engineering, the imaginary unit is denoted by the letter «j», since the letter «i» is already used here to denote current.

From Ohm's Law determines the complex value of the resistance:

Addition and subtraction of complex values ​​is done in algebraic form, and multiplication and division in exponential form.

Let's consider the method of complex amplitudes using the example of a specific circuit with certain values ​​\u200b\u200bof the main parameters.

An example of solving a problem using complex numbers

Given:

• coil voltage 50 V,

• resistor resistance 25 Ohm,

• coil inductance 500 mH,

• the electrical capacity of the capacitor is 30 microfarads,

• coil resistance 10 Ohm,

• mains frequency 50 Hz.

Find: ammeter and voltmeter readings as well as wattmeter.

Answer:

To begin with, we write down the complex resistance of series-connected elements, which consists of real and imaginary parts, then we find the complex resistance of an active-inductive element.

Remembering! To get the exponential form, find the modulus z equal to the square root of the sum of the squares of the real and imaginary parts, and phi equal to the arctangent of the quotient of the imaginary part divided by the real part.

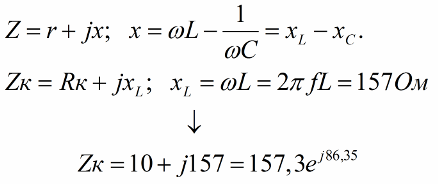
Then we find the current and, accordingly, the readings of the ammeter:

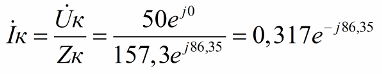
So the ammeter shows a current of 0.317 A—that's the current through the entire series circuit.

Now we will find the capacitive resistance of the capacitor, then we will determine its complex resistance:

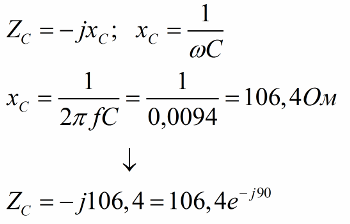
We then calculate the total complex impedance of this circuit:

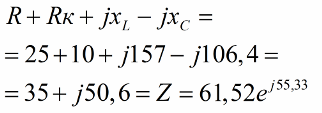
Now we find the effective voltage applied to the circuit:

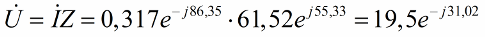
The voltmeter will show an effective voltage of 19.5 volts.

Finally, we find the power that the wattmeter will display, taking into account the phase difference between current and voltage

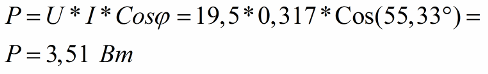
The wattmeter will show 3.51 watts.

Now you understand how important complex numbers are in electrical engineering. They are used for convenient calculation of electrical circuits. Many electronic measuring devices work on the same basis.