Oscillatory process in electrical engineering and electronics, types of oscillations
Oscillatory process — a process with varying degrees of repeatability. All oscillatory processes are divided into 2 classes: periodic and non-periodic. In theory, they also use an intermediate class—almost periodic oscillations.
An oscillatory process is called periodic, in which the value characterizing this process, taken at any time, after a certain period of time T has the same value.
The function f (t), which is a mathematical expression of the oscillatory process, is called periodic with period T if it satisfies the condition f (t + T) = f (t).
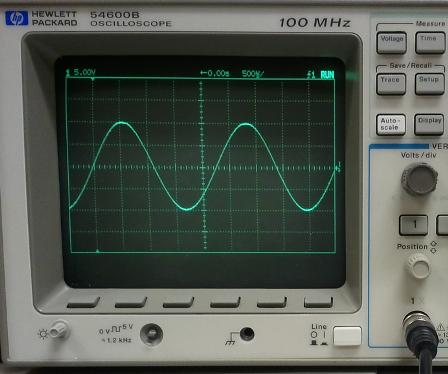
Among the class of periodic oscillatory processes, the main role is played by harmonic or sinusoidal oscillations, in which a change in a physical quantity with time occurs according to the law of sine or cosine. Their overall record is:
y = f (t) = aCos ((2π / T) t — φ),
where a — amplitude of oscillations, φ is the phase of oscillation, 1 /T = f — frequency and 2πf = ω — frequency of cyclic or circular vibrations.
Application of sinusoidal oscillations and their characteristics:
Graphical ways to display alternating current
An almost periodic function corresponding to a reading of periodic oscillations is defined by the condition:
| f · (t + τ) — f (t) | <= ε where ε — assign a value to each value T.
The quantity τ this case is called almost period. If the value ε is very small compared to the average value of f (t) at time T, then the quasi-periodic function will be close to the periodic one.
Non-periodic oscillations are much more varied than periodic ones. But most often in automation one has to meet damping or increasing sinusoidal oscillations.
Oscillations according to the law of the damped sinusoid or, as they are sometimes called, damped harmonic oscillations, can be represented in a general form:
x = Ae-δTcos·(ω + φ),
where t is time, A and φ are arbitrary constants. The general notation of the law of increasing harmonic oscillations differs only in the sign of the damping factor δ[1 second].
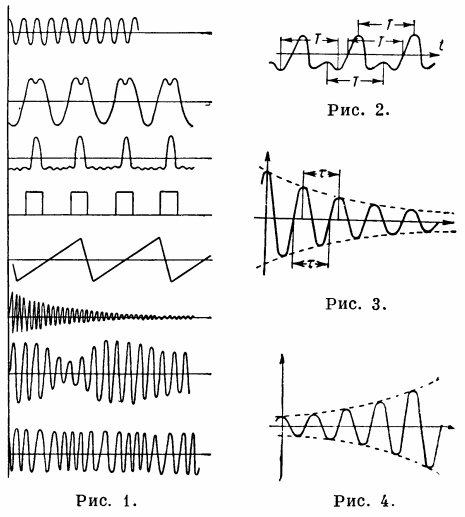
Fig. 1 — oscillating process, Fig. 2. — periodic process, fig. 3. — decaying harmonic oscillations, fig. 4. — increase in harmonic oscillations.
An example of the application of the oscillatory process is the simplest oscillatory circuit.
Oscillator circuit (electric circuit) — a passive electric circuit in which electrical oscillations can occur with a frequency determined by the parameters of the circuit itself.
The simplest oscillating circuit consists of capacitance C and inductance L. In the absence of external influence, damping oscillations with frequency εО = 1/2π√LC.
The amplitude of the vibrations decreases with eg-δT, where δ is the damping coefficient. If δ> = eO, then the damped oscillations in the circuit become non-periodic.
In electronics, the quality of the oscillating circuit is determined by the quality factor: Q = nf/δ... When an external periodic force acts on the oscillating circuit, forced oscillations occur in it. The amplitude of forced oscillations increases significantly for high-Q circuits if the frequency of the external influence is close to eo (resonance). Oscillating circuit is one of the main parts in resonant amplifiers, generators and other electronic devices.
See also on this topic: Application of voltage resonance and current resonance
