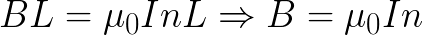The Biot-Savart law and the theorem of the circulation of the magnetic induction vector

In 1820, the French scientists Jean-Baptiste Biot and Félix Savard, in the course of joint experiments to study the magnetic fields of direct currents, unequivocally established that the magnetic induction of a direct current flowing through a conductor can be considered the result of the general action of all sections of this wire with current. This means that the magnetic field obeys the principle of superposition (the principle of superposition of fields).

The magnetic field created by a group of DC wires has the following magnetic inductionthat its value is defined as the vector sum of the magnetic inductions created by each conductor separately. That is, the induction B of the direct current conductor can be fairly represented by the vector sum of the elementary inductions dB belonging to the elementary sections dl of the considered direct current conductor I.

It is practically unrealistic to isolate an elementary section of a direct current conductor, because D.C. always closed.But you can measure the total magnetic induction created by a wire, that is, generated by all the elementary parts of a given wire.

Thus, Biot-Sovar's law allows you to find the value of the magnetic induction B of the section (known length dl) of the conductor, with a given direct current I, at a certain distance r from this section of the conductor and in a certain direction of observation from the selected section (set through the sine of the angle between the direction of the current and the direction from the section of the conductor to the examined point in the space near the conductor):

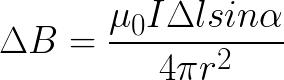
It was experimentally established that the direction of the magnetic induction vector is easily determined by the right-hand screw or gimbal rule: if the direction of translational movement of the gimbal during its rotation coincides with the direction of direct current I in the wire, then direction of rotation of the gimbal handle determines the direction of the magnetic induction vector B produced by a given current.

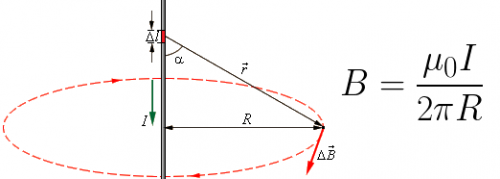
The magnetic field of a straight current-carrying wire, as well as an illustration of the application of Bio-Savart's law to it, are shown in the figure:

So, if we integrate, that is, add, the contribution of each of the small sections of a constant current conductor to the total magnetic field, we get a formula for finding the magnetic induction of a current conductor at a certain radius R from it.

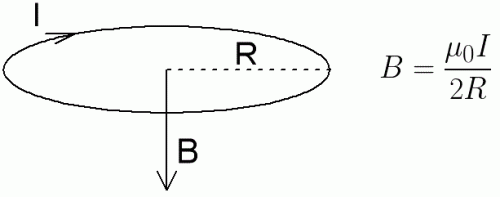
In the same way, using Bio-Savard's law, you can calculate the magnetic inductions from direct currents of different configurations and at certain points in space, for example, the magnetic induction in the center of a circular circuit with a current is found by the following formula:

The direction of the magnetic induction vector is easily found according to the gimbal rule, only now the gimbal must be rotated in the direction of the closed current, and the forward movement of the gimbal will show the direction of the magnetic induction vector.

Often calculations with respect to the magnetic field can be simplified if we take into account the symmetry of the configuration of currents given by the generating field. Here you can use the theorem of the circulation of the magnetic induction vector (like the Gauss theorem in electrostatics). What is «circulation of the magnetic induction vector»?

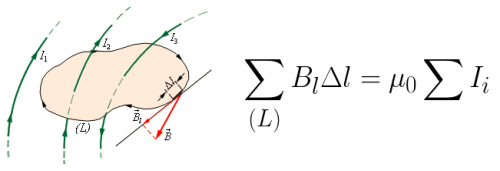
Let us choose in space a certain closed loop of arbitrary shape and conditionally indicate the positive direction of its travel. For each point of this loop, you can find the projection of the magnetic induction vector B on the tangent to the loop at that point. Then the sum of the products of these quantities by the elementary lengths of all sections of the contour is the circulation of the magnetic induction vector B along this contour:

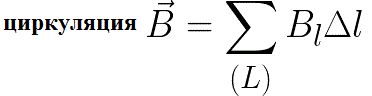
Practically all the currents that create a general magnetic field here can either penetrate the circuit under consideration, or some of them can be outside it. According to the circulation theorem: the circulation of the magnetic induction vector B of direct currents in a closed loop is numerically equal to the product of the magnetic constant mu0 by the sum of all direct currents that penetrate the loop. This theorem was formulated by Andre Marie Ampere in 1826:

Consider the figure above. Here, the currents I1 and I2 penetrate the circuit, but they are directed in different directions, which means that they have conditionally different signs.The positive sign will have a current whose direction of magnetic induction (according to the basic rule) coincides with the direction of the bypass of the selected circuit. For this situation, the circulation theorem takes the form:

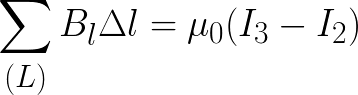
In general, the theorem for the circulation of the magnetic induction vector B follows from the magnetic field superposition principle and the Biot-Savard law.

For example, we derive the formula for the magnetic induction of a direct current conductor. Let us choose a contour in the form of a circle, through the center of which this wire passes, and the wire is perpendicular to the plane of the contour.

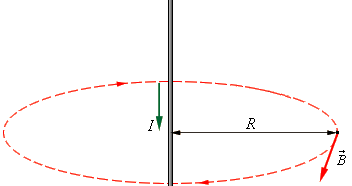
Thus the center of the circle lies directly in the center of the conductor, that is, in the conductor. Since the picture is symmetric, the vector B is directed tangentially to the circle, and its projection on the tangent is therefore the same everywhere and is equal to the length of the vector B. The circulation theorem is written as follows:

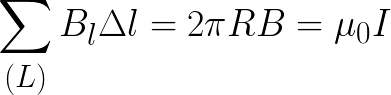
Therefore, the formula for the magnetic induction of a straight conductor with direct current follows (this formula has already been given above). Similarly, using the circulation theorem, one can easily find the magnetic inductions of symmetrical DC configurations where the picture of the field lines is easy to visualize.

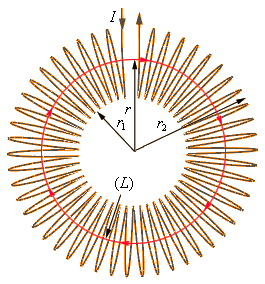
One of the practically important examples of the application of the circulation theorem is to find the magnetic field inside a toroidal inductor.

Suppose there is a toroidal coil wound round-to-round on a doughnut-shaped cardboard frame with the number of turns N. In this configuration, the magnetic induction lines are enclosed inside the doughnut and are concentric (within each other) circles in shape.

If you look in the direction of the magnetic induction vector along the inner axis of the donut, it turns out that the current is directed everywhere clockwise (according to the gimbal rule). Consider one of the lines (shown in red) of magnetic induction inside the coil and choose it as a circular loop of radius r. Then the circulation theorem for a given circuit is written as follows:

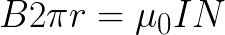
And the magnetic induction of the field inside the coil will be equal to:

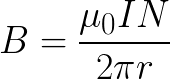
For a thin toroidal coil, where the magnetic field is almost uniform over its entire cross-section, it is possible to write the expression for the magnetic induction as if for an infinitely long solenoid, taking into account the number of turns per unit length — n :

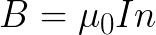
Consider now an infinitely long solenoid where the magnetic field is entirely inside. We apply the circulation theorem to the selected rectangular contour.

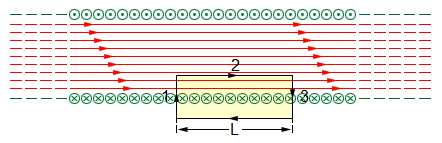
Here the magnetic induction vector will give a non-zero projection only on side 2 (its length is equal to L). Using the parameter n — «the number of turns per unit length», we get such a form of the circulation theorem, which ultimately reduces to the same form as for a multitonCoy toroidal coil: