Ohm's law in complex form

In the process of calculating electric circuits with an alternating sinusoidal current, Ohm's Law in complex form is often useful. An electric circuit here is understood as a linear circuit in a steady state of operation, that is, such a circuit in which the transient processes have ended and the currents are established.

The voltage drop, EMF sources, and currents in the branches of such a circuit are simply trigonometric functions of time. If, even in steady state, the current shape of the circuit is not a sinusoid (meander, sawtooth, impulse noise), then Ohm's law in complex form will no longer apply.

In one way or another, everywhere in the industry today it is used three-phase system with alternating sinusoidal current… The voltage in such networks has a strictly defined frequency and effective value. The effective value «220 volts» or «380 volts» can be found in the markings of various equipment, in the technical documentation for it. For this reason, because of such an obvious unification, Ohm's law in complex form is convenient in many electrical circuit calculations (where it is used in conjunction with Kirchhoff's rules).

The usual form of writing Ohm's law differs from the complex form of its recording. In complex form, the designations of EMF, voltages, currents, resistances are written as complex numbers… This is necessary to conveniently account for and perform calculations with both the active and reactive components that occur in AC circuits.

It is not always possible to simply take and divide the voltage drop by the current, sometimes it is important to take into account the nature of the circuit section and this forces us to make some additions to the mathematics.

The symbolic method (the complex number method) eliminates the need to solve differential equations in the process of calculating the electrical circuit of a sinusoidal current. Because in an AC circuit it happens, for example, that there is a current but no voltage drop in the circuit section; or there is a voltage drop but no current in the circuit while the circuit appears to be closed.

In DC circuits this is simply impossible. That's why for AC and Ohm's law is different. Unless there is a purely active load in a single-phase circuit, it can be used with almost no differences from DC calculations.

A complex number consists of an imaginary Im and a real Re part and can be represented by a vector in polar coordinates. A vector will be characterized by a certain modulus and an angle at which it rotates around the origin of the coordinates relative to the abscissa axis. The modulus is the amplitude and the angle is the initial phase.

This vector can be written in trigonometric, exponential, or algebraic forms.It will be a symbolic image of real physical phenomena, because in reality there are no imaginary and material characteristics in the schemes. It's just a convenient method for solving electrical problems with circuits.

Complex numbers can be divided, multiplied, added, raised to a power. These operations must be able to be performed in order to apply Ohm's law in complex form.

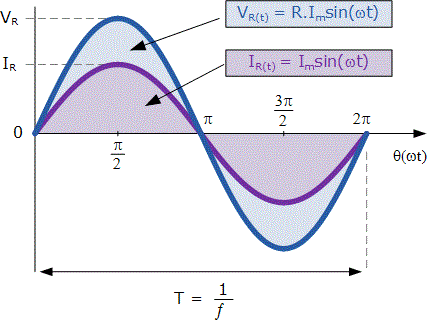
Resistances in alternating current circuits are divided into: active, reactive and common. In addition, conductivity must be distinguished. Electrical capacitance and inductance have AC reactants. Reactive resistance refer to the imaginary part, and the active resistance and conductivity - to the real part, that is, to the completely real.

Writing resistances in symbolic form makes some physical sense. In active resistance, the electricity is actually dissipated as heat together The Joule-Lenz law, while of capacitance and inductance, it is converted into electric and magnetic field energy. And it is possible to convert energy from one of these forms to another: from the energy of the magnetic field into heat, or from the energy of the electric field, partly into magnetic and partly into heat, and so on.

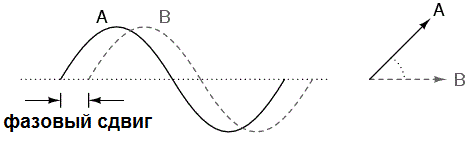
Traditionally, currents, voltage drops, and EMFs are written in trigonometric form, where both amplitude and phase are taken into account, which clearly reflects the physical meaning of the phenomenon. The angular frequency of the voltages and currents may differ; therefore, the algebraic form of notation is practically more convenient.

The presence of an angle between current and voltage leads to the fact that during oscillations there are times when the current (or voltage drop) is zero and the voltage drop (or current) is not zero. When the voltage and current are in the same phase, then the angle between them is a multiple of 180 °, and then if the voltage drop is zero, the current in the circuit is zero. These are instant values.

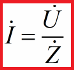
So, understanding the algebraic notation, we can now write Ohm's law in complex form. Instead of the simple active resistance (typical of DC circuits), the total (complex) resistance Z will be written here, and the effective values ​​of emf, currents and voltages will become complex quantities.

When calculating an electric circuit using complex numbers, it is important to remember that this method is only applicable to sinusoidal current circuits and is in steady state.