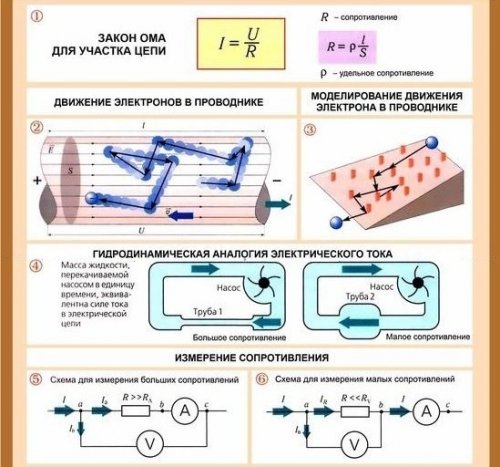
Ohm's law for a section of a circuit
The basic law of electrical engineering that you can use to study and calculate electrical circuits is Ohm's law, which establishes the relationship between current, voltage, and resistance. It is necessary to clearly understand its essence and be able to use it correctly in solving practical problems. Mistakes are often made in electrical engineering due to the inability to correctly apply Ohm's law.
Ohm's law for a section of circuit states: current is directly proportional to voltage and inversely proportional to resistance.
If the voltage acting in an electrical circuit is increased several times, the current in that circuit will increase by the same amount. And if you increase the resistance of the circuit several times, the current will decrease by the same amount. In the same way, the water flow in the pipe is the greater, the stronger the pressure and the smaller the resistance of the pipe to the movement of water.
In a popular form, this law can be formulated as follows: the higher the voltage for the same resistance, the higher the current, and at the same time, the higher the resistance for the same voltage, the lower is the amperage.
To express Ohm's law mathematically in the simplest possible way, the resistance of a wire carrying a current of 1 A at a voltage of 1 V is considered to be 1 Ohm.
Current in amperes can always be determined by dividing the voltage in volts by the resistance in ohms. Therefore, Ohm's Law for a section of a circuit is written in the following formula:
I = U / R.

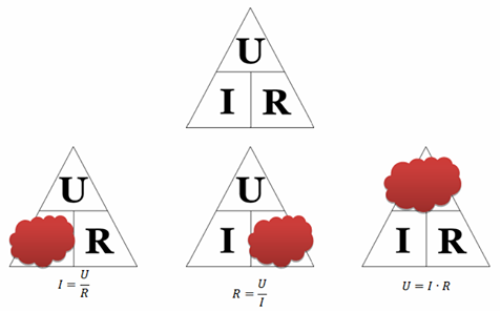
Magic triangle
Any section or element of an electric circuit can be characterized by three characteristics: current, voltage and resistance.
How to use Ohm's triangle: we close the required value — two other symbols will give the formula for its calculation. By the way, only one formula from the triangle is called Ohm's law - the one that reflects the dependence of current on voltage and resistance. The other two formulas, although they are consequences of it, do not make physical sense.
Calculations made using Ohm's law for a section of circuit will be correct when the voltage is in volts, the resistance is in ohms, and the current is in amperes. If multiple units of these quantities are used (e.g., milliamps, millivolts, megohms, etc.), they must be converted to amperes, volts, and ohms, respectively. To emphasize this, the Ohm's law formula for a section of a circuit is sometimes written as follows:
amp = volt / ohm
You can also calculate current in milliamps and microamps, while voltage should be expressed in volts and resistance in kilohms and megohms, respectively.
Other articles about electricity in a simple and affordable way:
What are voltage, current and resistance: how they are used in practice
How resistance depends on temperature
Sources of EMF and current: main characteristics and differences
Electric and Magnetic Field—What's the Difference?
Ohm's law is valid for every section of the circuit. If it is necessary to determine the current in a given section of the circuit, then it is necessary to divide the voltage acting in this section (Fig. 1) by the resistance of this section.
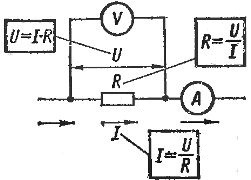
Figure 1. Application of Ohm's law to a section of circuit
Let us give an example of calculating the current according to Ohm's law... Let it be required to determine the current in a lamp with a resistance of 2.5 ohms, if the voltage applied to the lamp is 5 V. Dividing 5 V by 2.5 ohms, we get a value of current equal to 2 A. In the second example, we determine the current that will flow under the influence of a voltage of 500 V in a circuit whose resistance is 0.5 MΩ. To do this, we express the resistance in ohms. Dividing 500 V by 500,000 ohms, we find the current in the circuit, which is 0.001 A or 1 mA.
Often, knowing the current and resistance, the voltage is determined using Ohm's law. Let's write the formula to determine the voltage
U = IR
This formula shows that the voltage at the ends of a given section of the circuit is directly proportional to the current and the resistance... The meaning of this dependence is not difficult to understand.If the resistance of the circuit section does not change, the current can only be increased by increasing the voltage. This means that at constant resistance, a greater current corresponds to a greater voltage. If it is necessary to obtain the same current at different resistances, then with a higher resistance there must be a correspondingly higher voltage.
The voltage across a section of a circuit is often referred to as the voltage drop… This often leads to misunderstandings. Many people think that voltage drop is some wasted unnecessary voltage. In reality, the concepts of voltage and voltage drop are equivalent. Losses and Voltage Drops—What's the Difference?
Voltage drop is the gradual drop in potential across a current-carrying circuit due to the fact that the circuit has an active resistance. According to Ohm's law, the voltage drop in each section of the circuit U is equal to the product of the resistance of this section of the circuit R by the current in it I, i.e. U — RI. Thus, the greater the resistance of a section of the circuit, the greater the voltage drop in that section of the circuit for a given current.
The calculation of Ohm's law voltage can be shown in the following example. Let a current of 5 mA pass through a section of the circuit with a resistance of 10 kOhm, and it is necessary to determine the voltage in this section.
By multiplying A = 0.005 A at R — 10000 Ω, we obtain a voltage equal to 50 V. The same result can be obtained by multiplying 5 mA by 10 kΩ: U = 50 in
In electronic devices, current is usually expressed in milliamperes and resistance in kiloohms.Therefore, it is convenient to use exactly these units of measurement in calculations according to Ohm's law.
Ohm's law also calculates resistance if the voltage and current are known. The formula for this case is written as follows: R = U / I.
Resistance is always the ratio of voltage to current. If the voltage is increased or decreased by a number of times, the current will increase or decrease by the same number of times. The voltage-current ratio equal to the resistance remains unchanged.
The formula for determining resistance should not be understood to mean that the resistance of a given conductor depends on current and voltage. It is known to depend on the length, cross-sectional area and material of the wire. In appearance, the formula for determining resistance resembles the formula for calculating current, but there is a fundamental difference between them.
The current in a given section of the circuit really depends on the voltage and resistance and changes as they change. And the resistance of this section of the circuit is a constant value that does not depend on changes in voltage and current, but is equal to the ratio of these values.
When the same current flows in two sections of the circuit and the voltages applied to them are different, it is clear that the section to which the greater voltage is applied has a correspondingly greater resistance.
And if, under the action of the same voltage, a different current flows in two different sections of the circuit, then in this section there will always be a smaller current, which has a greater resistance.All this follows from the basic formulation of Ohm's law for a section of a circuit, that is, from the fact that the greater the current, the greater the voltage and the lower the resistance.
The calculation of resistance using Ohm's law for a section of a circuit will be shown in the following example. Let it be required to find the resistance of the section through which a current of 50 mA flows at a voltage of 40 V. Expressing the current in amperes, we get I = 0.05 A. Divide 40 by 0.05 and find that the resistance is 800 ohms.
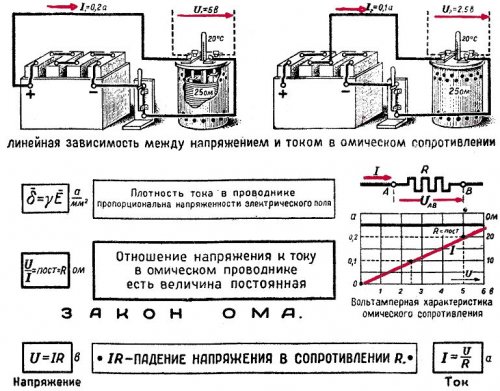
Ohm's law can be visualized in the form of the so-called current-voltage characteristic... As you know, the directly proportional relationship between two quantities is a straight line passing through the origin. This dependence is usually called linear.
In fig. 2 shown as an example graph of Ohm's law for a section of circuit with a resistance of 100 ohms. The horizontal axis is the voltage in volts and the vertical axis is the current in amperes. The current and voltage scale can be chosen as desired. A straight line is drawn so that for each of its points the voltage-to-current ratio is 100 ohms. For example, if U = 50 V, then I = 0.5 A and R = 50: 0.5 = 100 ohms.
Rice. 2… Ohm's Law (Current-Voltage Characteristic)
The graph of Ohm's law for negative values of current and voltage is the same. This implies that the current in the circuit flows the same way in both directions. The greater the resistance, the less current is obtained at a given voltage and the more carefully the straight line moves.
Devices in which the current-voltage characteristic is a straight line passing through the starting point, that is, the resistance remains constant when the voltage or current changes, are called linear devices... The terms linear circuits, linear resistances are also used.
There are also devices in which the resistance changes when the voltage or current changes. Then the relationship between current and voltage is expressed not according to Ohm's law, but in a more complex way. For such devices the current-voltage characteristic will not be a straight line passing through the starting point, but is either a curve or a dashed line. These devices are called non-linear.
See also on this topic: Application of Ohm's law in practice