Single phase alternating current

Acquiring alternating current

If the wire A is rotated in the magnetic flux formed by the two poles of the magnet in the clockwise direction (Fig. 1), then when the wire crosses the magnetic field lines, it will induce e. d. s whose value is determined by the expression

E = Blvsinα,

where B is the magnetic induction in T, l is the length of the wire in m, v is the speed of the wire in m / s, α — the angle at which the wire crosses the magnetic field lines.

Let B, I and v for this case remain constant, then the induced e. etc. c. will depend only on the angle α at which the wire crosses the magnetic field. So, at point 1, when the wire moves along the magnetic field lines, the value of the induced emf. etc. p will be zero when the wire moves to point 3 oe. etc. v. will be of the greatest importance, since the lines of force will be crossed by the conductor in the direction perpendicular to them, and finally, e.g. etc. v. will again reach zero if the wire is moved to point 5.

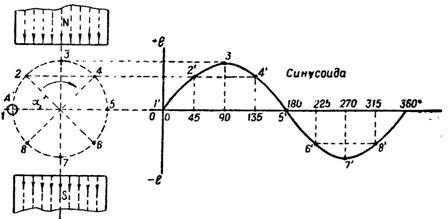
Rice. 1. Changing the induced e. etc. pp. in a wire rotating in a magnetic field

At intermediate points 2 and 4, in which the wire crosses the lines of force at an angle α = 45 °, the value of the induced emf. etc. c. will be correspondingly less than at point 3. Thus, when the wire is turned from point 1 to point 5, that is, by 180 °, the induced e. etc. v. changes from zero to maximum and back to zero.

It is quite obvious that on a further rotation of wire A through an angle of 180 ° (through points 6, 7, 8 and 1), the nature of the change in the induced e. etc. p. will be the same, but its direction will change to the opposite, since the wire will cross the magnetic field lines already under the other pole, which is equivalent to crossing them in the opposite first direction.

Therefore, when the wire is rotated 360 °, the induced e. etc. v. not only changes in magnitude all the time, but also changes its direction twice.

If the wire is closed to some resistance then the wire will appear electricity, also varying in size and direction.

Electric current, continuously changing in magnitude and direction, is called alternating current.

What is a sine wave?

The nature of the change e. etc. (current) for one turn of the wire for greater clarity, they are graphically represented using a curve. Since the value of e. etc. c. proportional to sinα, then, having set certain angles, it is possible, with the help of tables, to determine the value of the sine of each angle, and on the appropriate scale to construct a curve for the change of e. etc. c. To do this, on the horizontal axis we will set aside the angles of rotation of the wire, and on the vertical axis, in the appropriate scale, the induced e. etc. with

If previously indicated in fig.1 connect the points with a smooth curved line, then it will give an idea of ​​the magnitude and nature of the change in the induced e. etc. (current) at any position of the conductor in a magnetic field. Due to the fact that the value of the induced e. etc. p. at any moment is determined by the sine of the angle at which the wire crosses the magnetic field shown in fig. 1 curve is called a sinusoid, and e. etc. s. — sinusoidal.

Rice. 2. The sinusoid and its characteristic values

The changes we looked at e. etc. c. sinusoidally correspond to the rotation of the wire in a magnetic field at an angle of 360 °. When the wire is rotated the next 360 °, the changes in the induced e. etc. s.(and current) will appear again in a sine wave, that is, they will repeat periodically.

Accordingly, caused by this e. etc. c. is called electric current sinusoidal alternating current... It is quite obvious that the voltage that can be measured by us at the ends of wire A, in the presence of a closed external circuit, will also change in a sinusoidal manner.

Alternating current obtained by rotating a wire in a magnetic flux or a system of wires connected in a coil is called single-phase alternating current.

Sinusoidal alternating currents are the most widely used in technology. However, you can find alternating currents that do not change according to the sine law. Such alternating currents are called non-sinusoidal.

See also: What is alternating current and how does it differ from direct current

Amplitude, period, frequency of single-phase alternating current

Current strength, changing along a sinusoid, changes continuously. So, if at point A (Fig. 2) the current is equal to 3a, then at point B it will already be greater.At some other point on the sinusoid, for example at point C, the current will now have a new value, and so on.

The strength of the current at certain times when it changes along a sinusoid is called instantaneous current values.

The largest instantaneous value of a single-phase alternating current is called when it changes along a sinusoidal amplitude... It is easy to see that for one turn of the wire the current reaches its amplitude value twice. One of the values ​​of aa 'is positive and is drawn up from the 001 axis and the other bv 'is negative and is drawn down from the axis.

The time during which the induced e. etc. (or the current force) goes through the entire cycle of changes, the so-called monthly cycle T (Fig. 2). The period is usually measured in seconds.

The reciprocal of the period is called the frequency (f). In other words, alternating current frequency is the number of periods per unit time, i.e. in secondsdoo. So, for example, if an alternating current within 1 second assumes the same values ​​and direction ten times, then the frequency of such an alternating current will be 10 periods per second.

To measure frequency, instead of the number of periods per second, a unit called hertz (hertz) is used. A frequency of 1 hertz is equal to a frequency of 1 lps / sec. When measuring high frequencies, it is more convenient to use a unit 1000 times larger than the hertz, i.e. kilohertz (kHz), or 1,000,000 times greater than hertz — megahertz (mhz).

Alternating currents used in technology, depending on the frequency, can be divided into low-frequency currents and high-frequency currents.

AC rms value

Direct current passing through the wire heats it. If you run alternating current through the wire, the wire will also heat up.This is understandable, because although the alternating current changes its direction all the time, the release of heat does not depend at all on the direction of the current in the wire.

When alternating current is passed through a light bulb, its filament will glow. At a standard alternating current frequency of 50 Hz, there will be no flickering of the light, because the filament of the incandescent bulb, having thermal inertia, does not have time to cool down at those times when the current in the circuit is zero. The use of alternating current with a frequency of less than 50 Hz for lighting is now undesirable due to the fact that unpleasant, eye-fatiguing fluctuations in the intensity of the bulb appear.

Continuing the direct current analogy, we can expect that an alternating current flowing through a wire creates around it magnetic field. Actually nAlternating current does not create a magnetic field, but because the magnetic field it creates will also be variable in direction and magnitude.

An alternating current changes all the time in both magnitude and directionNS. Naturally, the question arises of how to measure the variable T well, and what its value when changing along a sinusoid should be taken as causing this or that action.

C For this purpose, alternating current is compared in terms of the action it produces with direct current, the value of which remains unchanged during the experiment.

Suppose that a direct current flows through a wire of constant resistance 10 A and it is found that the wire is heated to a temperature of 50 °.If now we pass through the same wire not a direct current, but an alternating current, and so we choose its value (acting, for example, with a rheostat) so that the wire is also heated to a temperature of 50 °, then in this case we can say that the action of alternating current is equal to the action of direct current.

Heating the wire in both cases to the same temperature shows that in a unit of time the alternating current gives off in the wire the same amount of heat as the direct current.

An alternating sinusoidal current that emits for a given resistance per unit time the same amount of heat as a direct current equivalent in magnitude to a direct current... This current value is called the effective (Id) or effective value of alternating current ... Therefore, for our example, the effective value of alternating current will be 10 A... In this case, the maximum (peak) current values ​​will exceed the average values ​​in magnitude.

Experience and calculations show that the effective values ​​of alternating current are smaller than its amplitude values ​​in √2 (1.41) times. Therefore, if the peak value of the current is known, then the effective value of the current Id can be determined by dividing the amplitude of the current Ia by √2, i.e. Id = Aza/√2

Conversely, if the rms value of the current is known, then the peak value of the current can be calculated, i.e. Ia = Azd√2

The same relations will hold for the amplitude and the rms values ​​of e. etc. v. and voltages: Unit = Ea /√2, Ud = Uа/√2

Measuring devices most often show the actual values, therefore, when notation, the index «d» is usually omitted, but you should not forget about it.

Impedance in AC circuits

When inductance and capacitance consumers are connected to the AC circuit, both active and reactance must be considered (reactance occurs when a capacitor is on or chokes in an AC circuit). Therefore, when determining the current passing through such a consumer, it is necessary to divide the supply voltage by the impedance of the circuit (consumer).

The impedance (Z) of a single-phase AC circuit is determined by the following formula:

Z = √(R2 + (ωL — 1 / ωC)2

where R is the active resistance of the circuit in ohms, L is the inductance of the circuit in henries, C is the capacitance of the circuit (capacitor) in farads, ω — angular frequency of alternating current.

Different consumers are used in alternating current circuits where it is necessary to consider either the three values ​​of R, L, C or only some of them. At the same time, the angular frequency of the alternating current must be taken into account.

For some users, only the values ​​of R and L can be taken into account at the corresponding corner frequency values. For example, at an AC frequency of 50 Hz solenoid coil or the generator winding can only be considered as containing active and inductive resistance. In other words, the capacitance in this case can be neglected. Then the AC impedance of such a user can be calculated by the formula:

Z = √(R2 + ω2L2)

If such a coil or a coil designed for alternating current operation is connected to a direct current of the same voltage, a very large current will flow through the coil, which can lead to significant heat generation, and the insulation of the coil can be damaged. On the contrary , a small current will flow through a coil designed to operate in a direct current circuit and connected to an alternating current circuit of the same voltage, and the device in which this coil is used will not perform the required action.

Resistance triangle, voltage triangle and power triangle: